Computational study of the transitional coherent structures in shear and centrifugally driven flows

Turbulence is not only omnipresent in our daily lives but also in engineering applications. However, not until the middle of the XXth century researchers began to realize that simple, relatively large-scale coherent structures are embedded, and play their part, in the seemingly totally random motion. These structures are recurrently visited in turbulent dynamics and play a key role in the transition to turbulence and in its sustenance. This thesis aims at identifying exact coherent structures in shear and centrifugal flows, studying their behavior and analyzing the corresponding dynamical relevance in turbulence, as well as their role in transition and in the phenomenon of intermittency (i.e., coexistence of laminar and turbulent flows).

In this research, direct numerical simulations are used to explore the rich dynamics of the Navier-Stokes equations. As a high dimensional dynamical system, turbulence can be regarded deterministically as a strange attractor embedded within the Navier-Stokes phase space, where exact coherent structures may be treated as invariant sets, and transitions can be explained in terms of bifurcation theory. The canonical flows chosen for this work are the Taylor-Couette system (flow between two coaxial cylinders counter-rotating with respect to their common axis), which embraces both centrifugal and shear instabilities, and the self-similar flows that arise between orthogonally stretching plates.

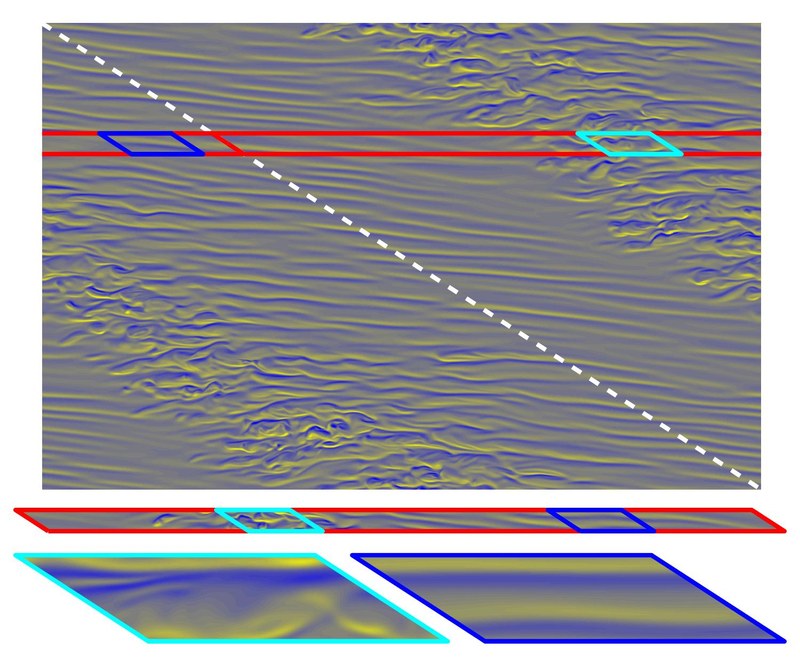
In the first part, we explore the mean structure of the spiral turbulence intermittent regime arising in the Taylor-Couette system. We manage to reduce drastically the computational cost by replacing the classical orthogonal domain by parallelogram-annular domains aligned in the direction of the turbulent spiral. In the second part, a series of drifting rotating wave solutions are tracked from the subcritical region, where the self-sustained process is proved to be at work, to the supercritical regime, where the spiral turbulence appears. The dynamical relevance of these wave solutions within spiral turbulence is studied in detail. The third part explores time-dependent flows arising between orthogonally stretching plates. In this case, many periodic and quasi-periodic flows are reported. In particular, phase-locking seems to be a quite generic phenomenon that inhibits the existence of chaotic dynamics. A strong resonance (1:4) is studied in detail and the results are consistent with the theoretical scenarios predicted by bifurcation theory.